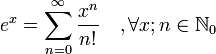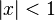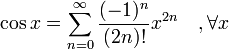4.1 Definición de serie
En matematicás, una serie es la suma de los términos de una sucesión. Se representa una serie con términos an como la imagen que se muestra en el costado izquierdo donde n es el índice final de la serie. En terminología matemática se incluye sucesión para designar la existencia de elementos encadenados o sucesivos. Se excluye totalmente la sinonimia con el término serie. Para entrar en materia la persona interesada en el tema debe de conocer el concepto de sucesión que se muestra a continuación:
El concepto de sucesión en los números reales se entiende de manera intuitiva cuando se asocia a un número natural un número real.
Termino de una sucesión: S: NàR
Normalmente las sucesiones son infinitas, y por lo general solo se enlistan los primeros 5 o 10 elementos, lo interesante de las sucesiones es que el estudiante observe los cambios significativos de un elemento a otro para encontrar un patrón que me sugiera encontrar la expresión matemática que los genera, para ello el alumno debe tener la habilidad de procedimientos algebraicos y de inducción matemática. En textos académicos se suele llamar simplemente sucesión con el bien entendido que todas son del mismo tipo. Esto no impide la existencia de sucesiones de diversas entidades matemáticas.
4.1.1 Finito
Las series tienen una características fundamental con respecto a su límite y esta es un parte aguas para generalizar o discriminar los tipos de series a grandes rasgos, series finitas o series infinitas, en esta parte en cuestión las series finitas son objeto de análisis.
 Observando la serie que se encuentra al costado izquierdo y mediante un análisis de sus componentes encontramos el límite superior determinado por “N”, esto significa que la serie esta superiormente acotada a cualquier numero natural, y por consecuente se puede deducir que es una serie finita puesto a que tiene un numero finito de elementos acotados por "N".
Observando la serie que se encuentra al costado izquierdo y mediante un análisis de sus componentes encontramos el límite superior determinado por “N”, esto significa que la serie esta superiormente acotada a cualquier numero natural, y por consecuente se puede deducir que es una serie finita puesto a que tiene un numero finito de elementos acotados por "N".4.1.2 Infinito
Una parte importante del estudio del Cálculo trata sobre la representación de funciones como “sumas finitas”. Realizar esto requiere extender la operación familiar de adición de un conjunto finito de números a la adición de una infinidad de números. Para llevar a cabo esto, se estudiara un proceso de limite en el que se consideran sucesiones.
Suponga que asociada a la sucesión
U1, U2, U3,…, Un,…
Se tiene una “suma infinita” denotada por
U1+ U2 + U3 +…+ Un+…
Pero ¿Qué es lo que significa esta expresión? Esto es, ¿Qué debe entenderse por la “suma” de n número infinito de términos, y en qué circunstancias dicha suma existe?
Teorema
Para tener una idea intuitiva del concepto de tal suma, suponga que un trozo de cuerda de 2 pie de longitud se corta a la mitad. Una de estas mitades de 1 pie de longitud se aparta y el otro y el otro se corta a la mitad otra vez. Uno de los trozos resultantes de ½ pie de longitud se aparta y el otro se corta a la mitad obteniéndose dos trozos, cada uno de 1/8 pie de longitud, otra vez, uno de los trozos se aparta y el otro se corta a la mitad. Si se continúa este procedimiento en forma indefinida, el número de pies de la suma de las longitudes de los trozos apartados puede considerarse como la suma infinita
1+ ½ + ¼ + 1/8+ 1/16 +…+ (1)/(2˄(N-1))
Como se inicio con un trozo de cuerda de 2 pie de longitud, nuestra intuición nos indica que la suma infinita (1) debe ser 2. Definiciones preliminares.
A partir de la sucesión
U1, U1, U3,…, Un,…
Se forma una nueva sucesión (Sn) sumando sucesivamente elementos de (Un):
S1=U1
S2=U1+U2
S3=U1+U2+U3
S4=U1+U2´+U3+U
…
Sn=U1+U2+U3+U4+…+Un
L a sucesión (An) obtenida de esta manera a partir de la sucesión (Sn) es una secesión de sumas parciales llamada serie infinita.
Definición de serie infinita
Si (Un) es una sucesión y Sn=A1+A2+A3+A4+…+Un
Entonces ( Sn) es una secesión de sumas parciales denominada serie infinita y se denota por
Los números A1, A2, A3,…, An,… son los términos de la serie infinita
Para un ejemplo presiso relacionado con el tema se sugiere el siguiente video instructivo:
4.2 Serie numerica y convergencia
*La serie armonica es la serie
La serie armónica es divergente
* Una serie añternada es una serie donde los términos alternan el signo. Ejemplo:
*Una serie telescópica es la suma donde an = bn − bn+1. Se representa de la siguiente manera:
La convergencia de dicha serie y su suma se pueden calcular fácilmente, ya que:
* Una serie hipergeometrica es una serie de la forma
que cumple que
Criterios de convergencia
Clasificar una serie es determinar si converge a un número real o si diverge ( u oscilante). Para esto existen distintos criterios que, aplicados a la serie en cuestión, mostrarán de que tipo es (convergente o divergente).
Condición del resto
Para que una serie sea divergente, una condición suficiente es que

Criterio de D'Alembert o Criterio del Cociente (Criterio de la razón)
Si existe
si L = 1, no es posible decir algo sobre el comportamiento de la serie.
Lo primero que miraremos cuando nos encontremos con una serie es si la ‘suma infinita’ tiene sentido:
La serie converge si lo hace su sucesion de sumas parciales; otra cosa distinta es que converja su termino general.
De la definicion y de las conocidas propiedades de los límites de sucesiones se deduce inmediatamente que si suprimimos, cambiamos o añadimos un numero finito de terminos al principio de una serie, no se altera su caracter de convergencia o divergencia (aunque si el valor de su suma, si converge), porque las nuevas sumas parciales diferiran de la inicial solo en un constante. Por eso, cuando estemos hablando simplemente de convergencia podremos no escribir el n en que empezamos a sumar; incluso escribiremos s olo “sigma” (no olvidando que son infinitos terminos).
Algunos tipos de series
* Una serie geometrica es una serie en la cual cada término se obtiene multiplicando el anterior por una constante, llamada razón. Ejemplo (con constante 1/2):
En general, una serie geométrica, de razón z, es convergente, sólo si |z| < 1, a:
Criterio de Raabe
En algunas series, puede ocurrir que ni el criterio de D'Alembert ni el de la raíz nos permitan determinar la convergencia o divergencia de la serie, entonces recurrimos al criterio de Raabe.
 Sea una serie como la mostrada tal que ak > 0 (serie de términos positivos). Y supongamos que existe
Sea una serie como la mostrada tal que ak > 0 (serie de términos positivos). Y supongamos que existeTened cuidado aquí, pues las conclusiones son al contrario que en los criterios de D'Alembert y de la raíz.
Convergencia absoluta
Una serie alternada an converge absolutamente si
Enlaces con ejercicios sobre el tema:
4.3 Series de potencias
Las series finitas que se han estudiado hasta este momento han consistido solo de términos constantes. Ahora se trata un tipo importante de series de términos variables denominadas series de potencias, las cuales pueden considerarse como una generalización de de una función polinomial. En las secciones restantes de este capítulo se estudiara como pueden emplearse las series de potencias para calcular valores de funciones tales como sean x, ln x y (x)˄1/2, las cuales no se pueden evaluar mediante las operaciones aritméticas conocidas y empleadas para determinar valores de funciones racionales.
Definición de una serie de potencias:
Una serie de potencias en x-a es una serie de la forma
Co+C1(x-c)+C2(x-c)˄2+…+Cn(x-c)˄n+…
Si la serie de potencias expuesta anteriormente es convergente para x= x1(x1diferente de 0), entonces es absolutamente convergente para todos los valores de x para los cuales [x]<[x1]
Una serie de potencias alrededor de x=0 es una serie de la forma:
Teorema
SI la serie de potencias expuesta con anterioridad es divergente para x=x2, entonces es divergente para todos los valores de x para los que [x]>[x2]
*Procedimiento para determinar el intervalo de convergencia de una serie de potencias x-a
1.Aplique el criterio de la razon (o en ocaciones el criterio de la raiz) para determinar el radio de convergencia R de la serie. Algunas series convergen absolutamente paratodos los valores de x.
2.- Si R>0, la serie converge absolutamente para toda x en el intervalo (a-R, a+R) y diverge para
[x-a]>R. Verifique la convergencia en los dos extremos del intervalo (a-R,a+R), por supuesto, nunguna conclucion acerca de la convergencia en los extremos puede inferirse del criterio de la razon o del criterio de la raiz.
4.4 Radio de convergencia
En matematicas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma
con
Definición
Si nos limitamos al conjunto de los numeros reales, una serie de la forma  , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
 , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
Ejemplos
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
 .
.(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.Distancia a la singularidad
El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x0 = 3 tiene la forma:
 .
.Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:
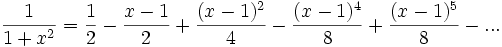
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es  . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
 . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serieRadio de convergencia infinito
Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho  .
.
 .
.y esto vale para todo real x por eso el radio de convergencia será infinito.
4.6 Serie de Taylor
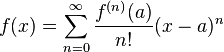
Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Definición
La serie de Taylor de una función f de numeros reales o complejos que es infinitamente diferenciableen un entrono de números reales o complejos a, es la serie de potencias:
series de Taylor en el siglo XVIII.
Series de Maclaurin (Taylor alrededor de 0) notables
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.Funcion exponencial y logaritmo natural
Serie geometrica
Teorema del binomio
y cualquierpara
 complejo
complejoFunciones trigonometricas
-
- Donde Bs son los Numero de Bernoulli.
4.5 Representacion de funciones mediante la serie de Taylor
sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1, 3, 5, 7, 9, 11 y 13
La función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).
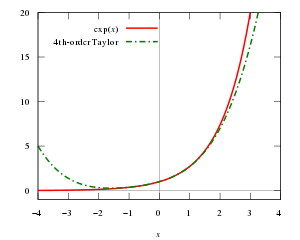
La función exponencial y = ex (línea roja continua) y su aproximación mediante un polinomio de Taylor alrededor del origen de (línea verde discontinua).
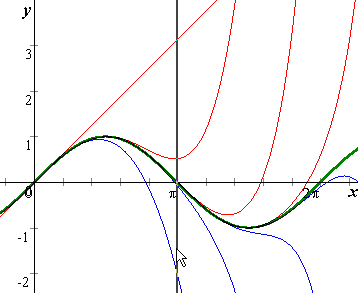

Puedes observar el comportamiento de aproximación usando algún polinomio de taylor por y = sin x.
El valor en x = π en cada función se despliegan al lado derecho.
El valor en x = π en cada función se despliegan al lado derecho.
4.7 Calculo de integrales expresadas como serie de Taylor
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:
f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio si se conocen los valores de f(a) y de sus n primeras derivadas.
Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)n. Además, es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)n.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.
Las leyes naturales pueden expresarse, por regla general, con buena aproximación por funciones derivables un número arbitrario de veces, y por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por la precisión deseada.
La fórmula de Taylor, que abre el camino para la mayoría de los cálculos en el análisis aplicado, es muy importante desde el punto de vista práctico.
La idea de aproximar una función mediante polinomios o de representarla como suma de un número finito de funciones más sencillas alcanzó un gran desarrollo en el análisis, donde constituye ahora una rama independiente: la teoría de la aproximación de funciones.
En las siguientes escenas podemos observar cómo la gráfica de las funciones se va "tapando" con la gráfica del polinomio de Taylor al aumentar el grado del polinomio. Para un valor de x calculamos la diferencia entre el valor real y el valor del polinomio correspondiente. Al aumentar el grado del polinomio esa diferencia es cada vez menor. Hemos calculado los polinomios de Taylor para a=0.
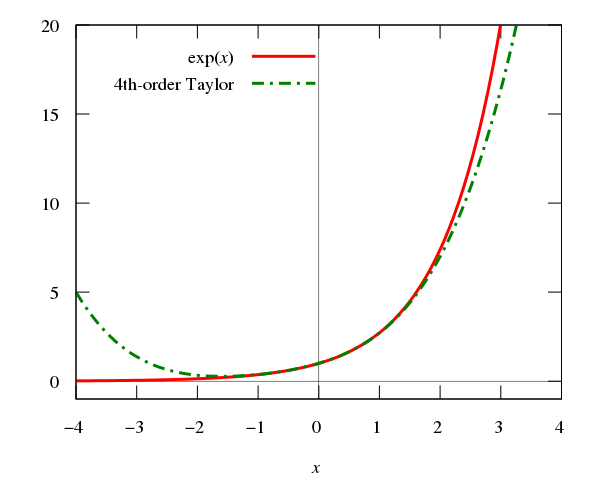
La función exponencial y = ex (línea roja continua) y su aproximación mediante un polinomio de Taylor alrededor del origen de (línea verde discontinua).